数学のはなし
本屋さんで、『数学でつまずくのはなぜか』という本を見つけた。
つまずきっぱ人間としては、実に気になる話。
かーなり期待して読んだ。
が、正直期待外れ( ̄、 ̄)
まず、誰を対象として書いたのかフメイ。
数学ダメ人間を対象とするにしては、内容が数学的過ぎるし、内容は既に試み尽されたことだから、数学教師を対象とするにはムリがある。
大体さ、そんなんじゃわからないから困ってるわけで\(-"-)/
そして、数学が好きで得意な人が自身の認識の枠組みで捉えたものを超えてはいなかった。
実感的に教えるとか、その工夫や努力も、数学が大好きなんだな~ってのも伝わってくるんだけど、それだけ。
なんとなくなんだけど、数学ダメ問題は、この著者が考えているよりも根が深いと思うんだ。
例えば私、今は四則演算すら怪しいけど、もともと数学全般ダメってわけじゃない。
得意不得意が極端で、偏差値で言えば上は60台後半から下は29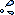
得意だったのは、集合、確率と代数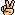
ダメなのは幾何、関数その他二次元三次元を相手にするもの全般。
ただ、某知能テストでは、二次元悲惨なくせに三次元はかなり高かったりするので、単純に次元の問題なのかどうかはわからない。
あと、運動を伴うものになると、そもそも脳まで信号がたどり着かないwww....._| ̄|○ il||li
根本的に認識ができないから、いくら噛み砕かれても意味ナイ(´;ω;`)
なんかね、もっと、まったく違うアプローチが必要なんだと思う。
よく言われることだけど、人間の認知の方法には差異があるわけ。
例えば道を歩くとき、自分が最初どちらを向いていて、何度曲がったから今はどちらを向いているということを、常に認識できている人がいる・・・らしいじゃん。
でも私には、それができない。
私は道を歩くとき、景色を一枚の絵、1つの映像として捉えている。
曲がろうが何しようが、景色が続く限りは一枚。
逆に言うと、「曲がる」っていう感覚が、存在しない。
「曲がる」を認識しようとするなら、自分を別の物体に置き換えて、第三者的かつ俯瞰的に捉えなきゃならない。
つまりさ、数学の認識の枠組みを持っている人が持っていない人のことを考えるには、限界があると思うわけ。
もちろん数学以外もそう。
だから、その教科が得意な人よりも苦手な人の方が教師に向いているっていうような意見も出てくるわけだけど、それはそれである面では真理であっても、ある面では虚なんじゃないかな。
その教科の凄さ、面白さを語れるのは、やっぱりその教科に精通した人間だろうしo(^-^)o
あ、それで、数学ダメ人間な私が数学のすごさを知ったできごとを1つ。
以前、数学が得意な友人に、こんな質問をした。
私:「微分(だったか積分だったか、はたまた複素数だったか失念)ってさ、結局何に使うわけ?何の役に立ってるわけ?」
友:「何の役に?うーん、いろいろあるけど・・・(なんか難しい話)」
私:「そんなんじゃわかんない(# ̄3 ̄)もっとわかりやすいの!あ、微分がなかったら、何ができないの?」
友:「クーラー作れないよ。あと冷蔵庫も。」
私:「うわっ!それは大変(lll゚Д゚)ヒィィィィ」
これだけで、私の中に微分⊂数学=すごい!っていう式が刻み付けられた。
それで出来るようになるわけじゃないけどさ(;^_^A
でもそういえばこういう話って、私は聞いたことがなかった。
聞かされる話といえば、物の動きとか距離とか、私のようなタイプにとってはそれだけで(″ロ゛)ヤメテーな話ばかり。
すごいってのはさ、大きな話からだけ感じ取れるもんでもないんだよ。
それこそ認知の型の違いってヤツ?
なんか・・・気がついたら長くなってた。
これ以上続けると際限なくなりそうなので、この辺にしとこ。
